واریانس و اندازه‌های پراکندگی — به زبان ساده

شاخص‌های آمار توصیفی، مانند شاخص‌های تمرکز و یا اندازه‌های پراکندگی به منظور شناخت جامعه آماری به کار می‌روند. ولی استفاده از هر یک به تنهایی ممکن است نتیجه مناسبی نداشته باشد. توجه همزمان به معیارهای تمرکز و پراکندگی کمک می‌کند که بهتر جامعه آماری شناخته شده و رفتار آن قابل مقایسه و تحلیل باشد. معیارهای تمرکز، نشان می‌دهند که داده‌ها، حول چه مقداری متمرکز هستند ولی بررسی نقطه تمرکز به تنهایی ممکن است محقق را به گمراهی بکشد.

مثال

فرض کنید نمرات دانشجویان دو مدرس در تدریس آمار طبق جدول زیر ثبت شده باشد.

مدرس	دانشجو۱	دانشجو۲	دانشجو۳	دانشجو۴	دانشجو۵	دانشجو۶	دانشجو۷	دانشجو۸	میانگین
مدرس الف	15	18	12	13	17	14	16	15	15
مدرس ب	10	18	20	10	20	20	12	10	15

  اگر برای ارزیابی دو مدرس از شاخص میانگین استفاده شود،‌ به نظر می‌رسد که هر دو دارای یک امتیاز باشند. در حالیکه دیده می‌شود در کلاس «مدرس الف» نمرات از یکدستی بیشتری برخوردار هستند و باوجود معدل ۱۵ در کلاس «مدرس ب»، نمرات پراکندگی بیشتری دارند که ممکن است نشان از عدم نظم در تدریس درس آمار داشته باشد. برای اینکه بتوان قضاوت بهتری برای ارزیابی این مدرس‌ها داشت، بهتر است علاوه بر شاخص میانگین از معیارهای دیگری مانند اندازه پراکندگی استفاده شود. در ادامه به معرفی چند اندازه پراکندگی می‌پردازیم که از شهرت بیشتری برخوردارند.

دامنه تغییرات

یکی از روش‌های اندازه‌گیری پراکندگی بین داده‌ها، محاسبه «دامنه تغییرات» (Range) است. این شاخص، حداکثر میزان پراکندگی را نشان می‌دهد و برای محاسبه آن کافی است که تفاوت بین بزرگترین و کوچکترین مقدار را بدست آورد. اگر دامنه تغییرات را با R نشان دهیم،‌ فرمول محاسباتی آن برای داده‌های a₁,a₂,a₃,a₄,a₅ به صورت زیر است: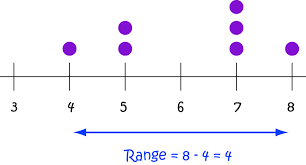

$$R=\text{Max}(a_1,a_2,a_3,a_4,a_5)-\text{Min}(a_1,a_2,a_3,a_4,a_5)$$

بنابراین طبق داده‌های جدول مربوط به نمرات دانشجویان که در بالا ذکر شد، میزان پراکندگی نمرات برای «مدرس الف» برابر با 6=12-18 نمره است در حالیکه برای «مدرس ب» 10=10-20 خواهد بود. مشخص است که میزان پراکندگی برای «مدرس ب» بیشتر است که نشان دهنده عدم توازن در تدریس او محسوب می‌شود.

مزایا و معایب

• مزایا
  • سادگی در محاسبه دامنه تغییرات
  • نمایش حداکثر میزان پراکندگی
• معایب
  • عدم محاسبه پراکندگی حول یک مرکز
  • تاثیر پذیری زیاد از مقادیر خیلی بزرگ و یا خیلی کوچک

هر چند سادگی محاسبات برای این شاخص از ویژگی‌های مهم آن است. ولی متاسفانه فقط بر اساس دو مقدار محاسبه می‌شود و بقیه مقدارها در تعیین این معیار نقشی ندارند.

 

دامنه میان چارکی

برای آنکه بتوان مشکل تاثیر پذیری دامنه تغییرات از مقدارهای بزرگ و کوچک را از بین برد، می‌توان فاصله بین بزرگترین و کوچکترین مقدار را براساس چارک‌ها محاسبه کرد. به این ترتیب برای داده‌هایی که دارای مقدارهای دور افتاده هستند، فاصله بین چارک اول و سوم، می‌تواند برآورد بهتری برای محاسبه حداکثر پراکندگی داده‌ها بدست دهد. به این شاخص «دامنه میان چارکی» (InterQuartile Range – IQR) می‌گویند. شکل محاسباتی دامنه میان چارکی به صورت زیر است:

$$IQR=Q3-Q1$$

که در آن Q₁ چارک اول و Q₃ چارک سوم است. برای مثال مربوط به داده‌های نمرات دانشجویان،‌ برای «مدرس الف» مقدار IQR = 2 و برای «مدرس ب» مقدار IQR = 10 خواهد بود که باز هم نشان‌دهنده عدم یکدستی نمرات برای «مدرس ب» است.

مزایا و معایب

• مزایا
  • عدم تاثیر پذیری زیاد از مقادیر خیلی بزرگ و یا خیلی کوچک (حذف اثرات نقاط دور افتاده)
  • سادگی در محاسبه (براساس مقدار چارک اول و سوم)
• معایب
  • عدم محاسبه پراکندگی حول یک مرکز
  • مقدارهای به جز چارک اول و سوم در محاسبه آن نقشی ندارند.

متوسط قدر مطلق انحرافات

معمولاً در صحبت‌های روزمره، زمانی که از فاصله یا پراکندگی صحبت می‌شود، می‌گویم این دو شهر نسبت به هم دور هستند یا روستاهای این استان نسبت به مرکز شهرستان فاصله زیادی دارند. همانطور که دیده می‌شود پراکندگی یا فاصله را نسبت به یک نقطه در نظر می‌گیریم. دامنه تغییرات و دامنه میان چارکی، معیارهای مناسبی برای اندازه‌گیری پراکندگی نیستند زیرا پراکندگی را نسبت به نقطه‌ای خاص در نظر نمی‌گیرند. برای رفع این مشکل بهتر است نقطه‌ای از داده‌ها را به عنوان مرکز در نظر گرفت و فاصله بقیه داده‌ها را نسبت به آن سنجید.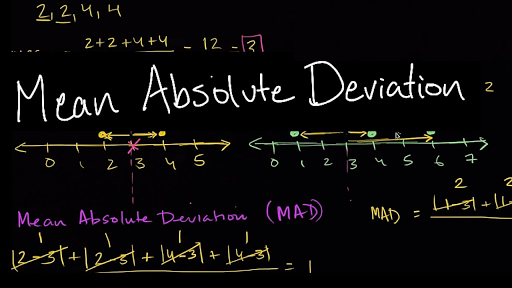 در محاسبه اندازه متوسط قدر مطلق انحرافات، اگر نقطه مرکزی، میانگین در نظر گرفته شود به آن «متوسط قدر مطلق انحرافات از میانگین» (Mean Deviation – MD) گفته می‌شود. البته ممکن است آن را با «قدر مطلق فاصله» (Absolute Difference from Mean – A.D) نیز نشان داد. برای محاسبه این شاخص کافی است میانگین داده‌ها محاسبه شده و قدر مطلق فاصله آن‌ها نسبت به میانگشان ثبت شود، سپس میانگین این فاصله‌ها حساب شود.

از آنجایی که میانگین، نقطه‌ای است که میانگین فاصله داده‌ها نسبت به آن صفر است، برای محاسبه MD از قدر مطلق فاصله‌ها استفاده می‌شود تا فقط مقدار فاصله، بدون در نظر گرفتن جهت آن، به کار رود. پس می‌توان فرمول محاسباتی زیر را برای MD یا A.D نوشت:

$$A.D=MD=\frac{\sum |x_i-\overline{x}|}{n}$$

نکته: اگر به جای میانگین از میانه به عنوان نقطه مرکزی استفاده شود به آن «متوسط قدر مطلق انحرافات از میانه» (Median Absolute Difference- MAD) می‌گویند. با توجه به تعریف میانه،‌ مشخص می‌شود که مجموع فاصله‌های $$x_i-a$$ به ازای قرار دادن میانه به جای a کمترین مقدار خود را خواهد داشت. فرمول محاسباتی برا‌ی MAD به صورت زیر است:

$$MAD=\frac{\sum |x_i-m|}{n}$$

براساس مثال نمرات دانشجویان میزان پراکندگی براساس میزان MD برای کلاس «مدرس الف» برابر با 1.5 و برای «مدرس ب» 4.5 خواهد بود. همچنین میزان پراکندگی بر منبای MAD‌ نیز برای «مدرس الف» و برای «مدرس ب» با مقدار MD آن‌ها برابر است (میانه و میانگین نمرات هر دو مدرس با هم برابر هستند).

مزایا و معایب

• مزایا
  • استفاده از یک نقطه‌ مرکزی برای سنجش انحرافات
  • نقش همه مقدارها در محاسبه پراکندگی
• معایب
  • تاثیرپذیری از مقدارهای خیلی بزرگ و یا خیلی کوچک
  • وابستگی به واحد اندازه‌گیری داده‌ها
  • پیچیدگی در استفاده از روش‌های ریاضی

نکته: اگر مقیاس اندازه‌گیری داده‌ها تغییر کند، یعنی همه مقدارها در عدد ثابت نامنفی ضرب یا تقسیم شوند،‌ مقدار دامنه تغییرات،‌ دامنه میان چارکی و MD یا MAD نیز در آن مقدار ضرب یا تقسیم خواهند شد ولی با اضافه یا کم شدن مقدار ثابت به داده‌ها، تغییری در این اندازه‌های پراکندگی بوجود نمی‌آید.

واریانس

از آنجایی که کارهای محاسباتی نظیر انتگرال و مشتق برای تابع قدر مطلق با مشکلاتی همراه است،‌ برای نامنفی کردن فاصله‌ها نسبت به میانگین، می‌توان از مربع آن‌ها استفاده کرد. به این صورتِ محاسبه میزان پراکندگی، «واریانس» (Variance) می‌گویند. اگر میانگین جامعه آماری را با $$\mu$$ نشان دهیم، شکل محاسباتی برای واریانس که با نماد Var یا $${\sigma }^2$$ مشخص می‌شود، به صورت زیر است.

$${\sigma }^2=Var(x)=\frac{\sum (x_i-\mu {)}^2}{n}$$

نکته: با توجه به تعریف میانگین و مشتق‌گیری می‌توان نشان داد که مجموع فاصله‌های $$(x_i-a{)}^2$$ به ازای قرار دادن میانگین به جای a کمترین مقدار خود را خواهد داشت.

فرمول ذکر شده در بالا برای محاسبه واریانس جامعه آماری به کار می‌رود. ولی اگر به جای جامعه آماری از یک نمونه آماری استفاده شود، ابتدا باید میانگین جامعه آماری ($$\mu$$) برآورد شود سپس واریانس نمونه برای برآورد واریانس جامعه آماری بکار رود. به این ترتیب اگر برای محاسبه واریانس نمونه، معلوم بودن میانگین نمونه را به عنوان یک محدودیت داشته باشیم، همه مقدارها به جز یکی می‌‌توانند آزادانه تغییر کنند. زیرا تغییرات داده‌ها باید به شکلی باشد که میانگین‌شان برابر با $$\overline{X}$$ باشد. به این ترتیب می‌گوئیم داده‌ها از n-1 درجه آزادی برخوردار هستند.

محاسبه واریانس نمونه‌ای که $$S^2$$ نشان داده می‌شود، کمی با واریانس جامعه متفاوت است، زیرا در مخرج به جای n‌ از n-1 استفاده شده است. شکل محاسباتی $$s^2$$ به صورت زیر است:

$$S^2=\frac{\sum (x_i-\overline{x}{)}^2}{n-1}$$

که در آن n-1 را درجه آزادی برای واریانس نمونه می‌گویند. اگر اندازه نمونه بزرگ شود، بین واریانس نمونه و جامعه آماری تفاوتی چندانی وجود نخواهد داشت زیرا n-1 به n‌ نزدیک می‌شود.

با توجه به مثال نمرات دانشجویان،‌ واریانس نمرات برای «مدرس الف» برابر با 3.5 و برای «مدرس ب» 21 است. اگر فرض شود که این کلاس‌ها نمونه‌ای از کلاس‌های این دو مدرس باشند، واریانس نمونه‌ای برای «مدرس الف» برابر با ۴ و برای «مدرس ب» ۲۴ محاسبه می‌شود.

نکته: اگر داده‌ها در مقدار ثابتی مثل b ضرب یا تقسیم شوند،‌ واریانس آن‌ها در b² ضرب یا تقسیم می‌شود ولی تغییر مکان داده‌ها در میزان واریانس آن‌ها تاثیری ندارد.

مزایا و معایب

• مزایا
  • قابلیت استفاده در بیشتر مفاهیم ریاضی
  • محاسبه پراکندگی حول میانگین
  • نقش همه داده‌ها در محاسبه میزان پراکندگی
• معایب
  • مربع شدن واحد اندازه‌گیری برای میزان پراکندگی
  • تاثیر پذیری زیاد از داده‌های بسیار بزرگ یا کوچک

انحراف معیار یا انحراف استاندارد

با توجه استفاده از توان ۲ در محاسبه واریانس، واحد اندازه‌گیری برای این شاخص به صورت مربع در خواهد آمد. برای مثال، اگر داده‌ها برحسب گرم باشند، واریانس برحسب گرم مربع (گرم به توان ۲)‌ خواهد بود. این موضوع باعث می‌شود که نتوان واریانس را با خود داده‌ها مقایسه کرد.

برای رفع این مشکل کافی است که جذر واریانس را محاسبه کنیم تا واحد اندازه‌گیری این شاخص پراکندگی با واحد اندازه‌گیری داده‌ها یکی شود. به حاصل این کار «انحراف معیار» (Standard Deviation) می‌گویند. انحراف معیار جامعه آماری با $$\sigma$$ و انحراف معیار نمونه S‌ نشان داده می‌شود.

پس شیوه محاسباتی برای انحراف معیار به صورت زیر خواهد بود؛

$$\sigma =\sqrt{{\sigma }^2}$$

$$S=\sqrt{S^2}$$

در مثال نمرات دانشجویان،‌ انحراف معیار نمرات برای «مدرس الف» برابر با 1.87 و برای «مدرس ب» 4.58 است. اگر فرض شود که این کلاس‌ها نمونه‌ای از کلاس‌های این دو مدرس باشند، انحراف معیار نمونه‌ای برای «مدرس الف» برابر با 2 و برای «مدرس ب» 4.9 محاسبه می‌شود.

نکته: اگر داده‌ها در مقدار ثابتی ضرب یا تقسیم شوند،‌ انحراف معیار آن‌ها نیز در همان مقدار ضرب یا تقسیم خواهد شد. در نتیجه تغییر مقیاس در داده‌ها باعث تغییر در انحراف معیار خواهد شد ولی تغییر مکان داده‌ها در میزان انحراف معیار آن‌ها تاثیری ندارد.

مزایا و معایب

• مزایا
  • قابلیت استفاده در بیشتر مفاهیم ریاضی
  • محاسبه پراکندگی حول میانگین
  • نقش همه داده‌ها در محاسبه میزان پراکندگی
  • قابلیت استفاده در بیشتر مقایسه‌های آماری
• معایب
  • تاثیر پذیری زیاد از داده‌های بسیار بزرگ یا کوچک
  • عدم ثبات در هنگام تغییر واحد داده‌ها

ضریب تغییرات

برای مقایسه پراکندگی دو گروه داده که با واحدهای اندازه‌گیری متفاوتی جمع‌آوری شده باشند،‌ استفاده از انحراف معیار،‌ واریانس، متوسط قدرمطلق انحرافات از میانگین، دامنه میان چارکی و دامنه تغییرات صحیح نیست. زیرا می‌دانیم که این اندازه‌ها با تغییر مقیاس داده‌ها، تغییر می‌کنند. برای رفع این مشکل از «ضریب تغییرات» (Coefficient of Variation- CV) استفاده می‌شود زیرا معیاری است که میزان نسبی پراکندگی را نشان می‌دهد.

برای محاسبه آن کافی است که نسبت انحراف استاندارد را به میانگین بدست آورد. از آنجایی که صورت و مخرج این کسر هم واحد هستند، حاصل کسر مقداری بدون واحد است که به صورت درصدی نیز می‌تواند بیان شود. بنابراین ممکن است برای یک سری داده گفته شود که ضریب تغییرات ۱۵٪‌ است. این امر به معنی آن است که انحراف معیار ۱۵ درصد میانگین است.

محاسبه ضریب تغییرات برای جامعه آماری به شکل زیر است:

$$CV=\frac{\sigma }{\mu }$$

و برای نمونه آماری به صورت زیر است:

$$cv=\frac{S}{\overline{x}}$$

اگر در مثال نمرات دانشجویان بخواهیم اثر سختی یا سادگی آزمون (‌که در میزان میانگین نهفته است) را از بین ببریم و پراکندگی را برحسب میانگین هر کلاس بسنجیم، کافی است ضریب تغییر را برای هر یک محاسبه کنیم. مدرسی که دارای ضریب تغییرات کمتری است، نمره‌های یکدست و همگنی داشته.

به این ترتیب ضریب تغییرات برای «مدرس الف» برابر با 12.47٪ و برای «مدرس ب» 30.55٪‌ است. اگر فرض شود که این کلاس‌ها نمونه‌ای از کلاس‌های این دو مدرس باشند، ضریب تغییرات نمونه‌ای برای «مدرس الف» برابر با 13.33٪ و برای «مدرس ب» 32.66٪ محاسبه می‌شود.

نکته: اگر داده‌ها در مقدار ثابتی ضرب یا تقسیم شوند،‌ ضریب تغییرات برای آن‌ها تغییر نخواهد کرد، در نتیجه تغییر مقیاس در داده‌ها تاثیری روی ضریب تغییرات ندارد. باید توجه داشت که برای محاسبه ضریب تغییرات لازم است داده‌ها کمی و از نوع نسبی باشند. محاسبه ضریب تغییرات برای داده‌های فاصله‌ای صحیح نیست.

مثال

دمای متوسط دو شهر در طول ۵ روز از سال برحسب سانتی‌گراد و فارنهایت در جدول زیر آورده شده است.

دمای شهرها	روز اول	روز دوم	روز سوم	روز چهارم	روز پنجم	میانگین	انحراف معیار	ضریب تغییرات
الف (سانتی‌گراد)	0	10	20	30	40	20	15.81	0.79
ب (فارنهایت)	32	50	68	86	10	68	28.46	0.42

با توجه به تفاوت واحد اندازه‌گیری دما در این دو شهر برای مقایسه میزان پراکندگی شاید ضریب تغییرات مناسب به نظر برسد. همانطور که دیده می‌شود «شهر ب» دارای ضریب تغییرات بیشتری است پس احتمال دارد این طور تصور شود که دما در آن به نسبت میانگین تغییرات زیادی دارد. ولی با توجه به اینکه دما با واحد سانتی‌گراد یا فارنهایت یک کمیت از نوع فاصله‌ای است،‌ استفاده از CV در اینجا صحیح نیست. (کمیت فاصله‌ای، کمیتی است که در آن صفر به صورت قراردادی در نظر گرفته می‌شود و به معنی هیچ نیست.)

اگر به جای سانتی‌گراد و فارنهایت از واحد کلوین برای دمای این دو شهر استفاده شود جدول زیر حاصل می‌شود. (برای تبدیل دمای سانتی‌گراد به کلوین مقدار 273.5 باید به همه داده‌ها اضافه شود. همچنین برای تبدیل فارنهایت به کلوین نیز دما برحسب فارنهایت را با 459.67 جمع کرده و نتیجه را به 1.8 تقسیم می‌کنیم.)

دمای شهرها (کلوین)	روز اول	روز دوم	روز سوم	روز چهارم	روز پنجم	میانگین	انحراف معیار	ضریب تغییرات
الف	273.5	283.5	293.5	303.5	313.5	293.5	15.81	0.054
ب	273.15	283.15	293.15	303.15	313.15	293.15	15.81	0.054

طبق این جدول دیده می‌شود که تغییرات دما نسبت به میانگین که همان ضریب تغییرات است، در «شهر الف» و «شهر ب» تقریبا یکسان است.

مزایا و معایب

• مزایا
  • نقش همه داده‌ها در محاسبه میزان پراکندگی
  • ثبات در هنگام تغییر واحد داده‌ها
  • امکان مقایسه بین دو گروه از داده‌ها با واحدهای متفاوت
• معایب
  • تاثیر پذیری زیاد از داده‌های بسیار بزرگ یا کوچک
  • پیچیدگی و طولانی بودن محاسبه
  • عدم قابلیت محاسبه برای داده‌های منفی
  • نامعتبر شدن مقدار ضریب تغییرات زمانی که میانگین به سمت صفر نزدیک شود