برآوردگر سازگار در آمار — به زبان ساده
برآوردگر سازگار در آمار
نوع خاصی از برآوردگرها آماری، «برآوردگر سازگار» (Consistent Estimator) یا «برآوردگر مجانبی سازگار» (Asymptotically Consistent Estimator)، است که براساس یک قاعده خاص، مقدار پارامتر جامعه ($\theta$) را تخمین میزند.
در این بین هر چه تعداد مشاهدات یا نمونه تصادفی افزایش پیدا کند، میزان نزدیکی برآوردگر به مقدار پارامتر بیشتر خواهد شد و به اصطلاح برآوردگر سازگار به مقدار پارامتر «همگرا در احتمال» (Converges in Probability) خواهد بود.
در عمل، برآوردگر سازگار، به عنوان تابعی از نمونه تصادفی و البته تعداد آنها (مثلا $n$) مشخص میشود. به همین علت معمولا برآوردگرهای سازگار را با اندیس $ n $ و به صورت دنبالهای از برآوردگرها مانند $ T_n $ در نظر میگیرند، بطوری که حد تابع $ T_n $ زمانی که تعداد نمونهها افزایش یابد، برابر با پارامتر $ \theta $ خواهد بود.
البته موضوع همگرایی و نوع آن برای نشان دادن نزدیکی برآوردگر به پارامتر باید به شکل دقیقتری بیان شود که البته در ادامه متن به آن خواهیم پرداخت. به نظر میرسد این تعریف، ارتباطی با مفهوم اریبی و نااریبی برآوردگرها نیز دارد. در حقیقت برآوردگر سازگار، برآوردگری است که در حد و با افزایش تعداد نمونهها، نااریب (Unbiased) بوده و میزان اریبی آن صفر میشود.
نکته: اگر دنباله برآورگرهای $T_n$ همگرا به پارامتر $ \theta $ نباشد، به آن «برآوردگر ناسازگار» (Inconsistent) میگویند.
تعریف برآوردگر سازگار در آمار
به طور رسمی، برآوردگر $ T_n $ برای پارامتر $ \theta $ را سازگار میگویند، اگر $ T_n $ در احتمال (In Probablity) به پارامتر $ \theta $ همگرا باشد.
این امر به این معنی است که توزیع دنباله برآوردگرها، به مقدار پارامتر نزدیک و نزدیکتر خواهد شد. بنابراین احتمال اینکه فاصله برآوردگر از پارامتر کمتر از هر مقدار دلخواهی باشد، برابر است با ۱. اگر $T_n$ یک برآوردگر سازگار برای $\theta$ باشد، آنگاه این موضوع را به بیان ریاضی به صورت زیر مینویسیم:
$ \large \lim_{n \to \infty} \Pr \left( |T_n – \theta | < \epsilon \right ) = 1 , \;\; \forall \epsilon > 0 $
رابطه ۱
نکته: گاهی همگرایی در احتمال را برای برآورد سازگار به صورتهای دیگری نیز نشان میدهند که بعضی از آنها را در ادامه مشاهده میکنید. این نمادها، همگی به معنی برقراری و صادق بودن برآوردگر $T_n$ در رابطه ۱ هستند.
$ \large T_n \xrightarrow {P} \theta , \;\;\;\;\; \; \text{plim } T_n = \theta $
از آنجایی که پارامتر $ \theta $، نامعلوم است، احتمال مربوط به رابطه ۱، باید برای همه اعضای فضای پارامتر نیز برقرار باشد. در نتیجه باید بوسیله یک تعریف دقیقتر، برآوردگر سازگار را معرفی کنیم.
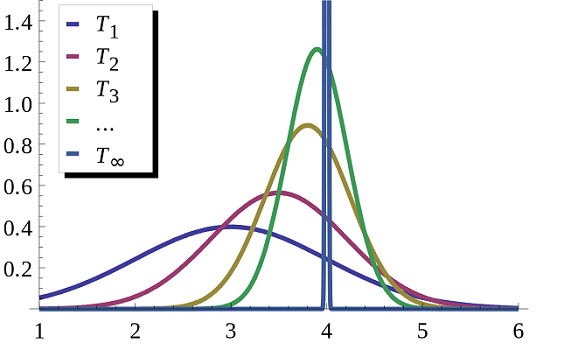
تعریف برآوردگر سازگار برای همه اعضای فضای پارامتری
فرض کنید $ \{p_{ \theta} \; : \; \theta \in \Theta\; \} $ خانوادهای از توزیعهای (مدل پارامتری) بوده و $ X^{\theta} = \{ X_1, X_2, \ldots : \; X_i \sim p_{\theta}\} $ نیز یک دنباله نامتناهی از نمونه تصادفی از توزیع $p_{\theta}$ باشد.
از طرفی دنباله برآوردگرهای $ \{T_n ( X^{\theta })\} $ را برای پارامتر $ g( \theta) $ در نظر بگیرید. آنگاه دنباله $ T_n $ را «سازگار ضعیف» (Weakly Consistent) برای $ g(\theta) $ گوییم اگر رابطه زیر برقرار باشد.
$ \large {\underset {n\to \infty }{ \operatorname {plim}}}\; T_{n} (X^{ {\theta } }) = g( \theta ) , \ \ \forall\ \theta \in \Theta $
رابطه ۲
همانطور که در رابطه ۲ مشاهده میکنید، برآوردگر $ T_n $ برای $ g ( \theta) $ به کار رفته است، چون در بعضی از مواقع لازم است تابعی از پارامتر را برآورد کنیم. به این ترتیب تعریف را برای هر تابعی از پارامتر، تعمیم دادهایم. اگر قرار باشد که فقط پارامتر توسط $ T_n $ برآورد شود، کافی است $ g(\theta) = \theta $ را در نظر بگیریم.
نکته: اگر همگرایی برآوردگر $ T_n $ به پارامتر $\theta$ به صورت «تقریبا مطمئن» (Almost Surely) باشد، برآوردگر $T_n$ را «سازگاری قوی» (Strong Consistent) گویند. در این حالت رابطه ۱ به صورت زیر در خواهد آمد.
$ \large \Pr \left( \lim_{ n \to \infty } T_n = \theta \right) = 1 $
رابطه ۳
در این حالت معمولا از نماد زیر برای نشان دادن سازگاری قوی استفاده میکنند. عبارت a.s مخفف Almost Surely یا «تقریبا مطمئن» است.
$ \large T_n \xrightarrow {a.s.} \theta $
پیدا کردن برآوردگر سازگار در آمار
در این قسمت با استفاده از تعریفی که برای سازگاری طبق رابطه ۱، معرفی کردیم، نشان خواهیم داد که میانگین نمونهای، یک برآوردگر سازگار برای میانگین توزیع نرمال ($ \mu $) است.
دنباله نمونه تصادفی $\{ X_1, X_2 , \ldots, \}$ از توزیع نرمال $ N(\mu,\sigma^2)$ را در نظر بگیرید که در آن واریانس ($\sigma^2$) معلوم و میانگین ( $ \mu$ ) نامعلوم است. به منظور برآورد پارامتر $ \mu $ از $n$ مشاهده اول $ X $ها استفاده کرده و برآوردگر $ T_n $ را براساس رابطه زیر ایجاد میکنیم.
$ \large T_n = \dfrac{ X_1 + X_2 + \ldots + X_n }{n} $
واضح است که $ T_n $، تابع از نمونه تصادفی و تعداد آنها است، به این معنی که $n$ ثابت نیست. با توجه به خصوصیات توزیع نرمال، میدانیم که توزیع نمونهای آماره $ T_n $ نیز نرمال خواهد بود.
$ \large T_n \sim N ( \mu \frac{ \sigma^2 }{n} ) $
پس باید مقدار احتمال زیر را برای سازگاری برآوردگر $ T_n $ محاسبه کنیم.
$ \large \Pr \! \left[\,| T_{n} – \mu |< \epsilon \,\right] $
با استفاده از استاندارد سازی (Standardize)، توزیع متغیر تصادفی (برآوردگر) $T_n$ را با یک تبدیل به توزیع نرمال استاندارد تغییر میدهیم.
$ \large {\displaystyle (T_{n} – \mu )/(\sigma /{ \sqrt {n} })} \sim N(0,1) $
در نتیجه داریم:
$ \large \Pr \left[\,|T_{n} – \mu | < \epsilon \,\right] = \Pr \! \left[{ \frac {{ \sqrt {n}} \,{\big |}T_{n} – \mu {\big |}}{\sigma } }< {\sqrt {n}} \epsilon /\sigma \right] $
با توجه به نماد $\Phi( )$ برای تابع توزیع تجمعی نرمال استاندارد، مقدار احتمال رابطه بالا برابر است با:
$ \large =\Pr \! \left[ {\frac {{\sqrt {n}} \,{\big |} T_{n} – \mu {\big | }}{\sigma }} < {\sqrt {n}}\epsilon /\sigma \right] = 2 \Phi \left({\frac {{\sqrt {n}} \, \epsilon }{\sigma } } \right) $
اگر از این احتمال برحسب $n$ حد بگیریم به رابطه زیر خواهیم رسید.
$ \large \lim_{n \to \infty} \Pr[ |T_n – \mu < \epsilon ] = \lim_{n \to \infty} \Phi(\frac{ \sqrt{n} \epsilon}{ \sigma}) = 1 $
که همان رابطه ۱ را برای هر $\epsilon$ ثابت و مثبت، نشان میدهد. پس میانگین نمونهای $T_n$ برآوردگر سازگار برای میانگین جامعه توزیع نرمال ($\mu$) است.
ایجاد برآوردگر سازگار در آمار
سازگاری برآوردگر هم از نظر نمادگذاری و هم از نظر تعریف، با مفهوم همگرایی در احتمال (براساس رابطه ۱) نزدیک است. در نتیجه همه ابزارهایی که برای همگرایی در احتمال وجود دارد، برای برآوردگر سازگار نیز به کار خواهد رفت. به این ترتیب قضیهها و نامساویهایی که برمبنای احتمال وجود دارند، برای نشان دادن سازگاری برآوردگرها مورد استفاده قرار خواهند گرفت. در ادامه به بعضی از آنها خواهیم پرداخت.
استفاده از نامساوی مارکف و چبیشف
در نوشتارهای دیگر مجله فرادرس با نامساوی مارکف (Markov Inequality) و نامساوی چبیشف (Chebyshev Inequality) آشنا شدهاید و میدانیم که این نامساویها برای مقدار احتمال تجمعی یک متغیر تصادفی، کران بالا ارائه میدهند. در اینجا قصد داریم به کمک آنها، سازگاری یک برآوردگر را نشان دهیم.
نامساوی زیر را در نظر بگیرید.
$ \large {\displaystyle \Pr \! {\big [} h(T_{n} – \theta ) \geq \epsilon {\big ]}\leq {\frac {\operatorname {E} {\big [} h(T_{n} – \theta ) {\big ]}} {h (\epsilon )} }} $
رابطه ۴
اگر در اینجا تابع $ h $ را قدر مطلق (Absolute Function) در نظر بگیریم، نامساوی مارکف و در صورتی که $ h $ را تابع درجه دوم (Quadratic Function) انتخاب کنیم، نامساوی چبیشف حاصل میشود. بنابراین کافی است، طرف راست رابطه ۴ را براساس هر یک از این توابع، محاسبه کرده و نشان دهیم که این مقدار برابر با صفر است.
نکته: توجه داشته باشید که رابطه ۴، متمم مقدار احتمال مربوط به رابطه ۱ را محاسبه کرده است. پس باید طرف راست به جای ۱ با صفر برابر باشد.
قضیه نگاشت پیوسته
فرض کنید دنبالهای از متغیرهای تصادفی $ \{X_n\} $ در اختیارمان هست. «قضیه نگاشت پیوسته» (Continuous Mapping Theorem)، بیان میکند که اگر دنباله $\{X_n\}$ به مثلا $ X $ همگرا باشند، آنگاه تحت شرایطی، تابعی از این دنبالهها مثل $ g(X_n) $ ها هم به همان تابع از همگرایی $X$ ها یعنی $ g(X) $ همگرا خواهد بود.
حال با نگاه برآوردگر سازگار به قضیه نگاشت پیوسته، توجه میکنیم. اگر $T_n$ یک برآوردگر سازگار برای $\theta$ بوده و $ g( \cdot)$ نیز تابعی حقیقی و پیوسته در $ \theta $ باشد، آنگاه $ g(T_n) $ نیز برای $ g( \theta) $ سازگار است. این موضوع به بیان ریاضی به صورت زیر نوشته میشود.
$ \large T_{n}\ {\xrightarrow {p}} \ \theta \ \quad \Rightarrow \quad g(T_{n})\ {\xrightarrow {p}}\ g(\theta ) $
نکته: شرط پیوستگی تابع $g$ در اینجا از اهمیت زیادی برخودار است و ممکن است بدون وجود این شرط، قضیه نگاشت پیوسته، برقرار نباشد.
قضیه اسلاتسکی
به کمک «قضیه اسلاتسکی» (Slutsky’s theorem)، بعضی از خواص جبری دنبالههای عددی به دنبالهای از متغیرهای تصادفی نیز نسبت داده میشود. به این ترتیب میتوان نشان داد که اگر دنباله متغیرهای تصادفی $\{X_n\}$ به $X$ و دنباله $\{Y_n\}$ به مقدار ثابت $c$ در توزیع همگرا باشند، آنگاه روابط زیر براساس همگرایی در توزیع (In Distribution) نیز برقرار خواهند بود.
$ \large X_{n} + Y_{n}\ { \xrightarrow {d}}\ X + c ;\\ \large { \displaystyle X_{n} Y_{n}\ { \xrightarrow d}}\ c X ;\\ \large { \displaystyle X_{n} / Y_{n}\ { \xrightarrow {d}}\ X/c , \;\; c \neq 0 } $
حال از این قضیه برای برآوردگر سازگار برای پارامتر $\theta$ استفاده میکنیم. $ \{ T_n \} $ و $ \{ S_n \} $ را دو دنباله از متغیرهای تصادفی در نظر بگیرید که برایشان داریم:
$ \large T_n \to \alpha \\ \large S_n \to \beta $
آنگاه روابط زیر نیز برقرار است.
$ \large { \displaystyle T_{n} + S_{n}\ { \xrightarrow {d}}\ \alpha + \beta } $
$ \large { \displaystyle T_{n} S_{n}\ { \xrightarrow {d}}\ \alpha \beta } $
$ \large { \displaystyle T_{n} / S_{n} { \xrightarrow {d}} \alpha /\beta ,\; \beta \neq 0 } $
نکته: نماد $\xrightarrow{d}$ نشانگر «همگرایی در توزیع» (Convergence in Distribution) است به این معنی که حد تابع توزیع دنباله متغیرهای تصادفی به یک توزیع خاص میل میکند. توجه داشته باشید که اگر همگرایی در احتمال وجود داشته باشد، همگرایی در توزیع نیز بدست خواهد آمد ولی عکس آن همیشه درست نیست. در نتیجه هنگام استفاده از قضیه اسلاتسکی باید با دقت بیشتر و توجه به شرایط برقراری همگرایی در احتمال، عمل کنید.
قانون اعداد بزرگ
اغلب فرم صریح برای برآوردگر $ T_n $ به صورت جمع یا تابعی از مجموع نمونههای تصادفی است. به این ترتیب استفاده از «قانون اعداد بزرگ» (Law of Large Numbers) که آن را به اختصار LLN میگویند نیز برای نشان دادن سازگاری برآوردگرها به کار میرود.
طبق قانون اعداد بزرگ برای یک دنباله از متغیرهای تصادفی $\{X_n\}$ تحت همتوزیعی و مستقل (iid) بودن، به شرط وجود امید ریاضی آنها ($ \mu $)، میتوان رابطه زیر را در نظر گرفت.
$ \large \frac{1}{n} \sum_{ i = 1 }^n X_i \xrightarrow {p} \operatorname{E} (X) = \mu $
به این ترتیب برای دنباله برآوردگرهای $ \{T_n\} $ هم که برآوردگر $ g(\theta) $ هستند، خواهیم داشت:
$ \large { \frac {1}{n}} \sum _{ {i = 1} }^{n} g(X_{i}) \ { \xrightarrow {p}} \ \operatorname {E} [\, g(X) \,] $
اریبی و ارتباط آن با برآوردگر سازگار در آمار
وجود «اُریبی» (Biased) برای یک برآوردگر در اکثر مواقع، عیب در نظر گرفته میشود و اغلب به دنبال یک برآوردگر نااُریب برای پارامتر مجهول جامعه هستیم. از طرفی سازگاری نیز به عنوان یک مزیت برای برآوردگر محسوب شده و علاقمند هستیم که برآوردگر نااریب، سازگار هم باشد.
در ادامه به این موضوع پرداخته و با استفاده از مثالهایی نشان میدهیم که ممکن است یک برآوردگر نااریب بوده ولی سازگار نباشد و برعکس برآوردگر اریبی پیدا کنیم که سازگار هم باشد. به همین دلیل، باید سازگاری و نااریبی را برای یک برآوردگر مورد تحقیق قرار دهیم.
برآوردگر نااریب ولی ناسازگار
در این قسمت، برآوردگری را معرفی میکنیم که در عین حال که نااریب است، ناسازگار هم است. مشاهدات مستقل و هم توزیع (iid) نمونه تصادفی $\{X_1,X_2,\ldots,X_n\}$ را در نظر بگیرید. فرض کنید که برآوردگر $\operatorname{E}(X)=\theta$ همان $T_n(X)=X_n$ باشد.
از آنجایی که $X$ها، همتوزیع هستند پس توزیع $ T_n(X) $ نیز با آنها یکی است و برای امید ریاضی (Mathematical Expectation) آن هم داریم:
$ \large \operatorname{E} (T_n) = \operatorname{E} (X_n ) = \theta $
پس برآوردگر $ T_n(X) $، یک برآوردگر نااریب است. ولی این برآوردگر، سازگار نیست، زیرا $ X_n $ به یک مقدار ثابت میل نمیکند. در نتیجه $ T_n $ برآوردگر سازگار برای $ \theta $ نخواهد بود.
البته در بیشتر موارد، برآوردگرهای نااریب، سازگار هم خواهند بود به شرطی که این برآوردگر به $n$ بستگی نداشته باشند.
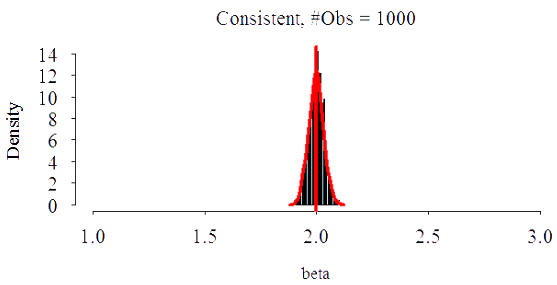
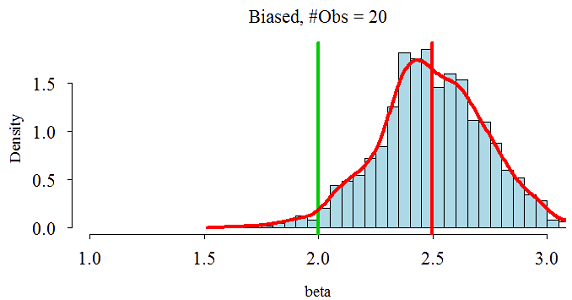
برآوردگر اریب ولی سازگار
فرض کنید میانگین یک توزیع از طریق برآوردگر زیر حاصل شود. البته در نظر داشته باشد که $\bar{X}$ یک برآوردگر نااریب برای $ \operatorname{E}(X) = \mu $ است.
$ \large T_n(X) = \frac{1}{n} \sum X_i + \frac{1}{n} = \bar{X} + \frac{1}{n} $
واضح است که $ T_n (X) $ یک برآوردگر اریب با مقدار اریبی $ \frac{1}{n} $ است. از آنجایی که میزان ارایبی $ T_n(X) $ در صورتی که اگر $ n $ به سمت بینهایت میل کند ($ n \to \infty $) برابر با صفر خواهد شد، پس $ T_n(X) $ نیز به $ \bar{X} $ میل کرده، در نتیجه سازگار است.
به عنوان یک مثال دیگر، به برآورد واریانس جامعه توسط واریانس نمونهای و انحراف معیار نمونهای میپردازیم. اگر واریانس نمونهای را به صورت زیر (بدون در نظر گرفتن ضریب اصلاح بسل – Bessel’s Correction) در نظر بگیریم، خواهیم داشت:
$ \large S^2_n(X) = \frac{1}{n} \sum_{i=1}^{n} (X_i – \bar{X})^2 $
قبلا نشان دادیم که این برآوردگر و جذر آن (انحراف معیار نمونهای) هر دو برآوردگرهای اریب (با اریبی منفی) هستند، زیرا:
$ \large \operatorname{E} \left( S^2_n(X) \right) = (1 – \frac{1}{n}) \sigma^2 < \sigma^2 $
ولی باید توجه داشت که این برآوردگر، سازگار هستند. مشخص است که با حد گرفتن از سمت چپ نامساوی بالا، زمانی که $n$ به سمت بینهایت میل کند، امید ریاضی $S^2_n(X)$ برابر با $\sigma^2$ خواهد بود. به این ترتیب هم برآوردگر نااریب و هم برآوردگر اریب برای واریانس جامعه، سازگار هستند.
این موضوع را با یک مثال دیگر به پایان میبریم. فرض کنید $T_n$ یک دنباله از برآوردگرهای $\theta$ با تابع احتمالی به فرم زیر باشد.
$ \large {\displaystyle \Pr ( T_{n}) = { \begin{cases}1 – 1/n, &{\mbox{if }}\,T_{n} = \theta \\ \large 1/n,& {\mbox{if }}\,T_{n} = n \delta + \theta \end{cases}}} $
واضح است که این برآوردگر دارای اریبی است.
$ \large E(T_n) = \theta \times (1-1/n) +1/n \times( n\delta + \theta) = \theta – \theta/n + \delta +\theta/n = \theta + \delta $
رابطه بالا به $n$ بستگی نداشته و در صورتی که $n \to \infty$، اریبی به سمت صفر میل نخواهد کرد. ولی از طرفی این برآوردگر سازگار است و داریم:
$ \large T_n \xrightarrow {p} \theta $
خلاصه و جمعبندی
در این نوشتار، با برآوردگر سازگار (Consistent Estimator) در آمار آشنا شدیم و با استفاده از چند مثال، کارایی چنین برآوردگرهایی را مشخص کردیم. در انتها نیز ارتباط نااریبی با سازگاری را مورد بررسی قرار دادیم. در این بین سازگاری ضعیف و سازگاری قوی را هم براساس همگرایی براساس احتمال (Convergence in Probability) یا تقریبا مطمئن (Almost Surely Convergence) مشخص کردیم.




