مفهومهای اصلی آمار که تحلیل گران علم داده باید بدانند
آمار، ابزاری موثر و قدرتمند برای انجام تحلیل داده محسوب میشود. هر چند بعضی معتقدند که علم داده یک هنر محسوب میشود ولی در آن از ابزارات علمی بسیاری زیادی کمک گرفته میشود. آمار به عنوان شاخهای از ریاضیات، در بسیاری از تحلیلهای مربوط به علم داده به کار میرود. شیوههای «تصویری سازی دادهها» (Data Visualization) که به کمک نمودارهای آماری صورت میپذیرد یکی از مراحل اولیه در عملیات تحلیل دادهها در نظر گرفته میشود. به عنوان مثال نمودارهایی مانند «نمودار میلهای» (Bar Chart)، نمودار دایرهای (Pie Chart) و … از شیوههای نمایش دادهها به شکل تصویری هستند که امکان انتقال اطلاعات را با سرعت بیشتری به کاربران میدهند. به این ترتیب به جای حدس و گمان در مورد اطلاعاتی که دادهها به ما میدهند میتوانیم آنها را در نمودارهای ترسیم شده به راحتی ببینیم. استفاده از آمار، امکان دریافت عمیقتر و درک شهودیتری از دادهها و رفتارشان به ما میدهد. در نتیجه انتخاب روش و تکنیکی که باید در علم داده به کار گرفته شود، راحتتر خواهد شد.
مفهومهای اصلی آمار
در این مطلب به بررسی پنج مفهوم یا روش آماری میپردازیم که هر تحلیلگر داده باید از آن اطلاع داشته تا در کارش بتواند موثرتر از قبل باشد. شیوه محاسبه بعضی از این شاخصهای آماری در مطلب مفاهیم آماری – شاخصهای توصیفی قابل مشاهده است.
1- شاخصهای آماری
انواع ویژگیها یا شاخصهای آمار توصیفی به عنوان یک مفهوم، از اهمیت خاصی برخوردار است. شناخت از انواع شاخصهای آماری و به کارگیری آنها روی دادههایی که میخواهید تحلیل کنید، اولین گام در اجرای تکنیکهای علم داده محسوب میشود. برای مثال اندازههای «میانگین» (Mean)، «اریبی» (Bias)، «واریانس» (Variance) و «چندکها» (Quantiles) میتوانند از شاخصهای آماری محسوب شوند. در تصویر زیر به یک نمونه از نمودارهای آماری اشاره شده است که به مقایسه بعضی از این شاخصها میپردازد. به این نمودار، «نمودار جعبهای» (Boxplot) یا «جعبه و خط» (Box and Whisker) گفته میشود.
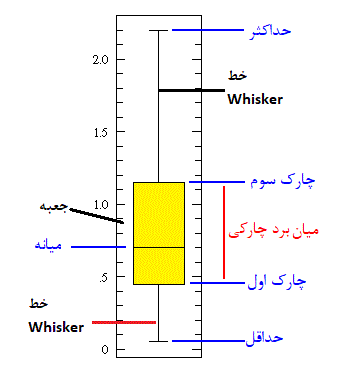
نمودار جعبهای – Boxplot
این نمودار که اولین بار توسط دانشمند آمار «توکی» (Tukey) معرفی شد دارای دو بخش «جعبه» (Box) و «خطوط» (Whisker) است. خطی افقی که در وسط جعبه در نمودار دیده میشود، میانه است که نسب به میانگین به دادههای پرت حساسیت کمتری دارد و مقاومتر است. چارک اول که همان صدک ۲۵ام است یکی از خطوط افقی پایینی نمودار است که بیانگر نقطهای است که ۲۵ درصد دادهها از آن کوچکتر هستند. از طرف دیگر چارک سوم نیز برابر با صدک ۷۵ است که نقطهای را نشان میدهد که ۷۵ درصد دادهها از آن کوچکتر هستند. این مقدار توسط یک خط افقی در قسمت بالای جعبه قرار گرفته است. همچنین فاصله بین حداقل و حداکثر (بیشترین و کمترین مقدار) که انتها و ابتدای خط عمودی (Whisker) را تشکیل میدهند، دامنه تغییرات کل را برای دادهها محاسبه و نشان میدهد. به عنوان یک برآورد مقاوم در برابر دادههای پرت، حداکثر میزان پراکندگی را میتوان براساس «دامنه بین چارکی» (Inter Quartile Range) نیز محاسبه کرد. گاهی این مقدار را با IQR نشان داده و به نام «میان برد چارکی» نیز معرفی میکنند. طول جعبه در این نمودار همان IQR است. نمودار جعبهای بطور کامل شاخصهای آماری مهم و موثر را محاسبه و نمایش میدهد. برای درک بهتر این نمودار به نکات زیر دقت کنید.
- اگر ارتفاع جعبه در این نمودار کوتاه باشد، متوجه میشویم که دادهها همگن و مشابه هستند زیرا تعداد زیادی داده در یک ارتفاع کوتاه قرار گرفتهاند.
- اگر قسمت جعبه نمودار دارای ارتفاع زیادی باشد، خواهیم فهمید که پراکندگی در دادهها زیاد و دامنه تغییرات برایشان بزرگ است. بنابراین تنوع دادهها زیاد خواهد بود.
- نزدیک بودن میانه (Median) به انتهای نمودار، بیانگر زیاد بودن تراکم دادهها در مقدارهای کم است. برعکس، اگر تمایل میانه به انتهای نمودار باشد، متوجه خواهیم شد که بیشتر دادهها، مقدارهای بزرگی هستند و تراکم دادههای کوچک، کمتر است. هر دو این حالات، نشانگر وجود چولگی در دادهها است. همچنین اگر میانه درست در وسط نمودار قرار بگیرد، تقارن در دادهها وجود داشته و میزان چولگی صفر محسوب خواهد شد.
- طولانی بودن «خطوط انتهایی» (Whiskers) (پایینتر از چارک اول و بالاتر از چارک سوم) بیانگر وجود واریانس یا انحراف استاندارد بزرگ است. بنابراین دادهها پراکندگی زیادی دارند. اگر یکی از خطوط انتهایی طولانیتر از دیگری باشد، پراکندگی دادهها در آن جهت رخ داده است. برای مثال اگر خط انتهای بالایی نمودار کشیدهتر از پایینی باشد، میزان پراکندگی دادههای بزرگ بیشتر از دادههای کوچک است.
همه این اطلاعات در یک نمودار ساده آماری جمعآوری شده است. این شیوه نمایش با وجود سادگی بیشترین اطلاعات را نشان میدهد که با دیدن خود دادهها هرگز بوجود نمیآمد. در حقیقت، هنر و اهمیت رسم نمودار در اینجا به وضوح دیده میشود.
2- توزیعهای احتمال
معمولا به شکل ساده، احتمال را شانس رخداد یک پیشامد برحسب درصد بیان میکنند. در علم داده، این مقدار به جای درصد به صورت عددی بین ۰ تا ۱ مشخص میشود. مقدار ۰ برای احتمال، نشانگر عدم رخداد و مقدار ۱ نشان دهنده رخداد قطعی یک پیشامد است. در این حالت، توزیع احتمال، تابعی است که مقدار احتمال را برای هر پیشامد آزمایش تصادفی نشان میدهد.
توزیع یکنواخت (Uniform Distribution)
این توزیع، یکی از مهمترین و کاربردیترین توزیعهای احتمالی در علم داده محسوب میشود. مقداری در فاصله پارامترهای این توزیع یعنی (a,b) را در نظر بگیرید. مقدار احتمال برای وقوع چنین مقداری برابر با
اگر تعداد حالات مقداری که این توزیع میتواند اختیار کند بیشتر از ۲ حالت باشد، به شکل تابع چند ضابطهای نوشته خواهد شد.
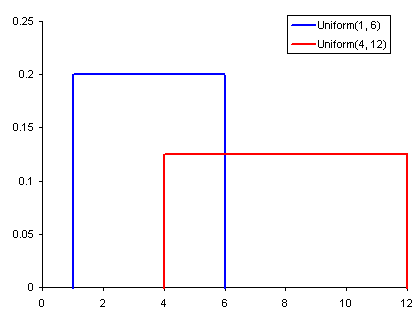
نکته: مشخص است که متغیر تصادفی یکنواخت معرفی شده در رابطه بالا، از نوع پیوسته محسوب میشود، زیرا تکیهگاه آن اعداد حقیقی است.
توزیع نرمال (Normal Distribution)
این توزیع احتمال به نام «توزیع گاوسی» (Gaussian Distribution) نیز شناخته شده است. پارامترهای این توزیع که توسط آن شناسایی میشود، میانگین (
میتوان شکل تابع احتمال چنین متغیر تصادفی را به صورت زیر نوشت:
که در آن
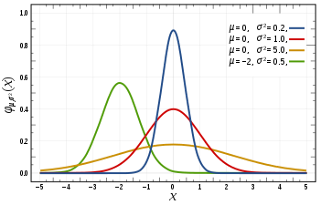
نکته: مشخص است که متغیر تصادفی نرمال معرفی شده در رابطه بالا، از نوع پیوسته محسوب میشود، زیرا تکیهگاه آن اعداد حقیقی است.
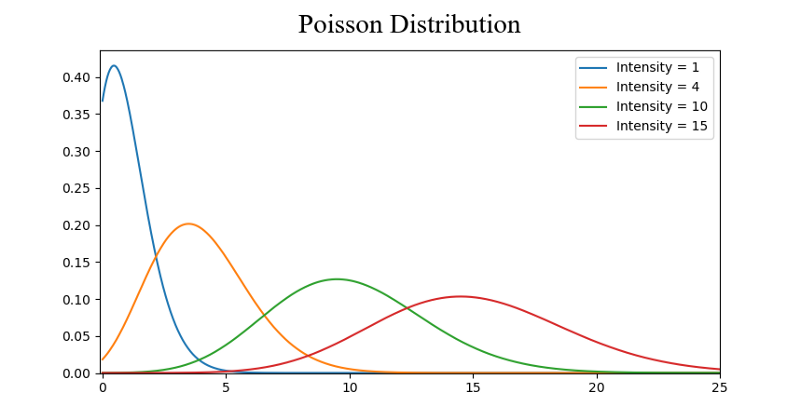
توزیع پواسن
شکل منحنی احتمال برای این توزیع به مانند توزیع نرمال است با این تفاوت که میزان پراکندگی نسبت به نقطه مرکزی در دو طرف منحنی یکسان نیست و دارای مقداری چولگی به سمت چپ است. به این ترتیب به نظر میرسد که تراکم دادهها در یک طرف زیاد و در طرف دیگر کم است. با افزایش پارامتر این توزیع، از میزان چولگی کاسته و به توزیع نرمال نزدیک میشود.
شکل تابع احتمال برای چنین متغیر تصادفی به صورت زیر است:
نکته: برای این متغیر تصادفی، مجموعه مقادیر یا تکیهگاه، اعداد طبیعی هستند. در نتیجه آن را میتوان یک متغیر تصادفی گسسته در نظر گرفت.
3- کاهش بعد
هرچند واژه «کاهش بعد» (Dimensionality Reduction) به نظر قابل فهم میآید ولی روش اجرای آن در آمار پیچیده و البته با بار محاسباتی زیاد همراه است. فرض کنید که با یک مجموعه داده مواجه هستید که دارای ابعاد زیادی است. در حقیقت در اینجا، خصوصیات اندازهگیری شده برای هر مشاهده زیاد و گسترده است. روش کاهش بعد کمک میکند که با متغیرهای کمتری برای تحلیلهای مربوط به علم دادهها مواجه باشید. برای آشنایی با این روش آماری، به تصویر زیر توجه کنید.
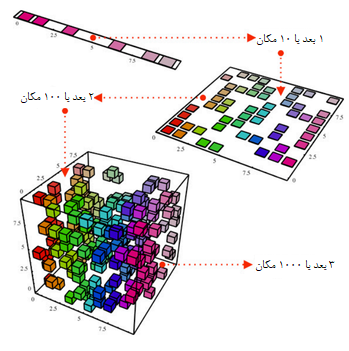
استفاده از ابعاد کمتر: فرض کنید مکعب بالا، مجموعه داده را در سه بعد نشان میدهد که گنجایش ۱۰۰۰ نقطه را دارد. یعنی هر نقطه میتواند با سه مولفه مشخص شود. با این حجم اطلاعات ممکن است محاسبات بسیار زمانبر و طولانی شوند. با توجه به نمایش اطلاعات به صورت دو بعدی، میتوان رنگها را ملاک تفکیک نقاط در نظر گرفت. پس عملاً وجود بعد سوم برای طبقهبندی دادهها مناسب نیست. اگر از فضای دو بعدی به فضای یک خط (یک بعدی) دادهها توجه کنیم، گروهبندی مناسب، ممکن است با خطای قابل اغماض و بار محاسباتی کمتر، حاصل شود.
حدف ابعاد غیر مرتبط: شیوه دیگر برای کاهش بعد، با «هرس کردن ویژگی» (Feature Pruning) صورت میگیرد. ویژگیهایی که بیشترین پراکندگی را بیان میکنند، مشخصات موثر در شناخت دادهها محسوب میشوند. در بیشتر تحلیلهای علم داده، به بررسی رابطه بین متغیرهای توصیفی (explanatory variable) و «پاسخ» (Respond) میپردازیم. بنابراین اگر بعضی از متغیرها یا ویژگیها توصیفی دارای همبستگی کم با متغیر پاسخ باشند، بهتر است که آنها را حذف کرده و محاسبات را براساس متغیرهایی توصیفی انجام داد که بیشترین وابستگی را با متغیر پاسخ دارند.
روش تحلیل مولفههای اصلی: معمولترین روش آماری برای کاهش بعد یک مسئله، استفاده از تکنیک تحلیل مولفههای اصلی (Principal Component Analysis) است. این روش به PCA معروف بوده و در روشهای مربوط به علم دادهها، بسیار به کار میرود. با استفاده از این روش، ترکیبهای خطی از متغیرهای توصیفی ایجاد میشود که بیشترین وابستگی را با متغیر پاسخ دارند. به هر یک از این ترکیبات، یک مولفه میگویند. میزان همبستگی بین مولفهها بسیار کم است بطوری که در اکثر موارد میتوان آن را صفر در نظر گرفت. این شیوه کاهش بعد هر دو عمل قبلی که به عنوان تقلیل یا کاهش بعد معرفی شد را بصورت یکجا انجام میدهد.
4- بیشنمونهگیری و کمنمونهگیری
یکی از تکنیکها و روشهایی که در مسائل طبقهبندی به کار میرود، روش «بیشنمونهگیری و کمنمونهگیری» (Over and Under Sampling) است. گاهی دادههای طبقهبندی شده تمایل به قرارگیری در یک گروه را دارند. برای مثال فرض کنید ۲۰۰۰ مشاهده برای گروه ۱ و ۲۰۰ مشاهده برای گروه دوم در مجموعه داده ثبت شدهاند. از روش «یادگیری ماشین» (Machine Learning) که یکی از تکنیکهای علم داده محسوب میشود، برای شناسایی اعضای این دو گروه استفاده میکنیم. مشخص است وجود تعداد مشاهدات بیشتر در یکی از گروهها، نتایج یادگیری ماشین را تحت تاثیر بیشتری قرار خواهد داد و برعکس گروهی که تعداد مشاهدات کمتری دارد، نمیتواند در نتایج تاثیرگذار باشد. برای روشنتر شدن موضوع به تصویر زیر توجه کنید.
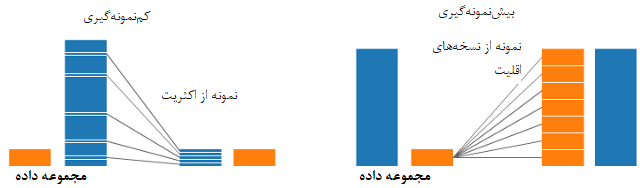
در هر دو تصویر سمت راست و چپ، گروه آبی دارای مشاهدات بیشتری نسبت به گروه نارنجی هستند. در این حالت، دو روش پیشپردازش برای انجام مراحل مدل یادگیری ماشین وجود دارد.
کمنمونهگیری: کمنمونهگیری به معنی انتخاب تعداد مشاهدات از گروه اکثریت به تعداد گروه اقلیت است. در حالیکه تعداد این نمونه باید با توجه به تابع احتمال انجام شود. به این ترتیب نقش گروه نارنجی و آبی در برآوردها یکسان خواهد شد.
بیشنمونهگیری: بیشنمونهگیری به معنی ایجاد نسخههایی از گروه اقلیت است تا بتوان تعداد اعضای نمونه را برای گروه آبی و نارنجی یکسان در نظر گرفت. این کار را میتوان به صورت نمونهگیری با جایگذاری یا بازنمونهگیری انجام داد.
5- آمار بیز
اگر درک درستی از آمار بیز و روشهای آن داشته باشیم، متوجه میشویم که در چه جاهایی آمار برمبنای فراوانی دچار مشکل میشود. آمار برمبنای فراوانی (Frequency Statistics) شاخهای از آمار است که بیشتر به نام احتمال شناخته شده است. در این بخش به محاسبه احتمال برای پدیدهها پرداخته میشود و فقط از اطلاعات مشاهده شده در مورد آن پدیده استفاده شود.

برای مثال، پرتاب یک تاس را در نظر بگیرید. اگر بخواهیم احتمال مشاهده ۶ را در پرتاب این تاس محاسبه کنیم کافی است که برای مثال ۱۰ هزار بار آن را پرتاب کرده و تعداد دفعاتی که شش مشاهده شده را بر ۱۰هزار تقسیم کنیم. با استفاده از این روش مقدار احتمال مشاهده عدد شش روی تاس تقریبا برابر
برعکس در آمار بیز احتمال رخداد یک پیشامد، علاوه بر مشاهدات به اطلاعاتی اضافهای که وجود دارد نیز پرداخته میشود. بنابراین شکل محاسبه احتمال برمبنای بیز به صورت احتمال شرطی است.
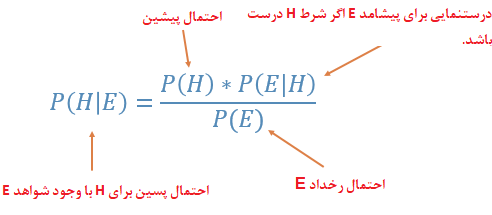
همانطور که دیده میشود احتمال پیشین یعنی
حال با به مسئله تاس برمیگردیم. اگر میخواهید میتوانید ۱۰هزار بار تاس را بیاندازد ولی اگر در هزار پرتاب اول مشاهده کردید که همیشه شش دیده شده، متوجه خواهید شد که تاس سالم نیست. به این ترتیب اگر
در نتیجه میتوان دید که در آمار بیز هم به شواهدی که توسط دادهها وجود دارد اهمیت داده شده و هم از اطلاعات قبلی که در دسترس بوده استفاده شده است. بنابراین بهتر میتوان به کمک آمار بیز دست به قضاوت زد. البته استفاده از آمار بیز، زمانی موثر است که اساسا در مورد یک پیشامد اطلاعات قبلی وجود داشته باشد.