چولگی — تعاریف و شیوه محاسبه
در تئوری احتمال و آمار، چولگی بیانگر میزان عدم تقارن توزیع احتمال دادهها حول میانگینشان است. مقدار چولگی میتواند منفی یا مثبت باشد. ممکن است تصور شود میزان تمایل منحنی توزیع احتمال یک سری داده، چولگی است ولی این معیار بیانگر عدم تقارن در دمهای این منحنی است. در حالتی که دادهها دارای توزیع متقارن باشند میزان کشیدگی دمهای سمت راست و چپ یکی است.
ابتدا «کارل پیرسون» (Karl Pearson) مفهوم چولگی و شیوه محاسبه آن را در سال 1895 ابداع کرد. البته او روشهای مختلفی برای بدست آوردن ضریب چولگی معرفی کرد که بتواند عدم تقارن را در توزیعهای مختلف نشان دهد.
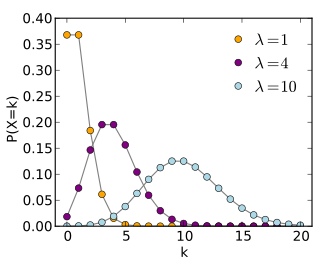
بعضی از توزیعهای آماری متقارن بوده و میزان چولگی برای آنها صفر است. بعضی از این توزیعها در جدول زیر معرفی شدهاند.
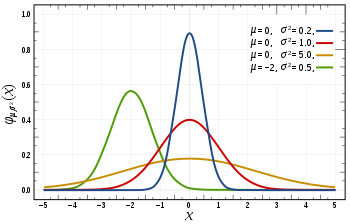 | 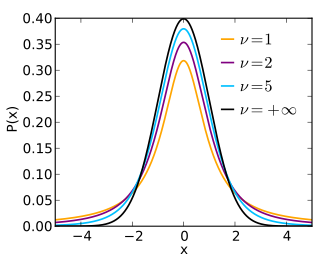 |
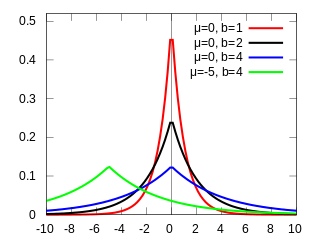 | 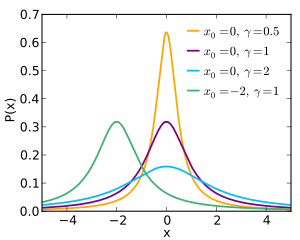 |
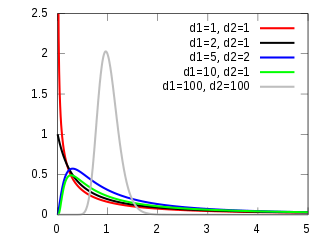
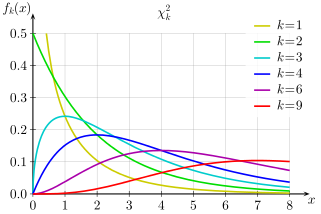
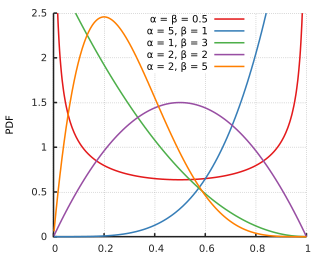
باید توجه داشته باشیم که در توزیعهای آماری نامتقارن، میزان چولگی مخالف صفر است. در جدول زیر بعضی از این توزیعها آورده شده است.
 |  |
 |  |
تعریف چولگی
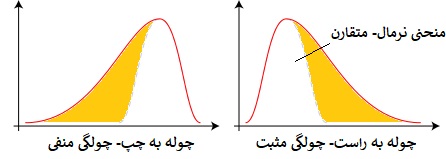
در تصویر شماره ۱ دو منحنی از توزیع احتمال دادهها ترسیم شده است. شکل خط منحنی در انتهای سمت راست با انتهای سمت چپ متفاوت است. قسمتهای انتهایی منحنی توزیع دادهها «دم» (Tail) نامیده میشود. از شکل این دمها میتوان چولگی توزیع را تشخیص داد.
در حالتی که دادهها «یک نمایی» (Unimodal) باشند و دم منحنی توزیع احتمال به سمت راست کشیده شده باشد به اصطلاح میگویند توزیع چوله به راست است. و برعکس اگر دم سمت چپ طولانیتر از سمت راست باشد توزیع دادهها چوله به چپ خواهد بود. تصویر شماره ۱ گویای این رابطه است. بنابراین گاهی به میزان چولگی، «پارامتر شکل» (Shape Parameter) نیز گفته میشود.
البته تفسیر شهودی چولگی مشکل است زیرا عدم تقارن ممکن است در اثر وجود حجم داده بیشتر در یک دم منحنی نیز بوجود آید. در این حالت منحنی را «دم سنگین» (Fat Tail) میگویند. دم سنگینی هم ممکن است به معنی چولگی در نظر گرفته شود. ولی به هر حال عدم تقارن ممکن است در اثر سنگین بودن یک دم و طولانی بودن دم دیگر بوجود آید.
نکته: برای دادههایی که دارای چند نما هستند تفسیر چولگی نیز بسیار سخت و پیچیده است.
نوع چولگی براساس اینکه مقداری مثبت یا منفی داشته باشد، مشخص میشود.
- چولگی منفی یا چوله به چپ: در این حالت دم سمت چپ طولانیتر از دم سمت راست است و حجم داده بیشتری در سمت راست متمرکز شده و به نظر میرسد که منحنی به سمت راست خمیده است. ولی از آنجایی که دم سمت چپ کشیدهتر است، اصطلاح چوله به چپ به کار میرود. در این حالت میانگین به سمت چپ منحنی تمایل پیدا میکند.
- چولگی مثبت یا چوله به راست: اگر دم سمت راست طولانیتر از دم سمت چپ باشد، منحنی توزیع دادهها را چوله به راست میگویند. هر چند در این حالت منحنی به سمت چپ خمیده شده و دادههای بیشتری در سمت چپ حضور دارند ولی طولانی شدن دم سمت راست باعث نامگذاری این حالت شده است. در این حالت میانگین به سمت راست تمایل بیشتری دارد.
از آنجایی که میزان چولگی بستگی به مقدار و تعداد نقاط روی دمها دارد، اضافه یا کم کردن مقداری به عنوان بزرگترین یا کوچکترین داده، روی میزان چولگی تاثیر گذار است. برای مثال اگر به دادههای 49، 50، 51 که حول میانگین ۵۰ متقارن هستند، مقدار 40 اضافه شود، تا دنبالهی 40،49،50،51 ایجاد شود، توزیع دادهها دارای چولگی به سمت چپ (چولگی منفی) خواهد بود. همچنین اگر دنباله دادههای قبلی را به صورت 49،50،51،60 دربیاوریم چولگی به سمت راست (چولگی مثبت) در شکل توزیع دادهها بوجود خواهد آمد.
نکته: ممکن است به اشتباه گفته شود ترتیب قرارگیری معیارهای تمرکز میانگین، میانه و نما نشاندهنده چولگی به راست یا چپ است. گاهی در کتابهای درسی گفته شده که اگر ترتیب قرارگیری این سه معیار از چپ به راست، میانگین، میانه و نما باشد، نوع چولگی راست است و در حالت برعکس چولگی به چپ است. این استدلال در حالتی که توزیع دادهها دارای چند نما یا توزیع گسسته باشد درست نیست و باید برمبنای محاسبه، میزان و چهت چولگی را بدست آورد.
ضریب چولگی گشتاوری پیرسون
اگر X یک متغیر تصادفی با میانگین $$\mu$$ و واریانس $$\sigma^2$$ باشد ضریب چولگی گشتاوری به صورت زیر محاسبه میشود.
$$\gamma_1=E[(\dfrac{X-\mu}{\sigma})^3]=\dfrac{\mu_3}{\sigma^3}$$
که در آن $$\mu_3$$ گشتاور مرکزی سوم است.
بنابراین اگر لازم باشد براساس یک نمونه آماری، ضریب چولگی گشتاوری را بدست آورد باید واریانس و گشتاور مرکزی سوم نمونهای را مبنا قرار داد. پس فرمول زیر را برای محاسبه ضریب چولگی گشتاوری نمونهای پیرسون خواهیم داشت.
$$b_1=\dfrac{m_3}{s^3}=\dfrac{\tfrac{1}{n}\sum(x_i-\overline{x})^3}{(\dfrac{1}{n-1}\sum(x_i-\overline{x})^2)^\tfrac{3}{2}}$$
با فرض داشتن مقدارهای «میانگین» (Mean)، «میانه» (Median)، «نما» (Mode) و «انحراف استاندارد» (S) میتوان ضریب چولگی سادهتری از جنبه محاسباتی بدست آورد.
ضریب چولگی اول پیرسون
ضریب چولگی اول پیرسون طبق رابطه زیر تعریف میشود که در آن نما مبنا در نظر گرفته شده است و انحراف میانگین از نما برحسب انحراف استاندارد محاسبه شده است.
$$\dfrac{Mean-Mode}{S}$$
البته گاهی به آن «چولگی نمای پیرسون» (Pearson Mode Skewness) نیز میگویند.
ضریب چولگی دوم پیرسون
ضریب چولگی دوم پیرسون اختلاف بین میانگین و میانه را مبنا قرار داده و نسبت آن را به انحراف استاندارد محاسبه میکند که گاهی آن را «چولگی میانه پیرسون» (Pearson Median Skewness) نیز مینامند.
$$\dfrac{3(Mean-Median)}{S}$$
نکته: اگر توزیع متقارن باشد میانگین و میانه برابر خواهند بود و ضریب گشتاوری دوم پیرسون برابر با صفر محاسبه خواهد شد.
چولگی برمبنای چارکها
اگر از چندکها برای محاسبه چولگی استفاده شود، شکل محاسباتی به صورت زیر خواهد بود. مشخص است که چارک دوم همان میانه است. این معیاز توسط «آرتور بولی» (Arthur Bowley) دانشمند آماری در سال ۱۹۰۱ معرفی شده است.
$$B_1=\dfrac{Q_3+Q_1-2Q_2}{Q_3-Q_1}$$
همانطور که دید میشود در مخرج کسر برای برآورد انحراف معیار از نصف فاصله بین چارک اول و سوم (دامنه میان چارکی) و در صورت کسر نیز میانگین چارک اول و سوم به عنوان برآورد میانگین محسوب شده است. زیرا با ساده کردن عبارت زیر به فرمول $$B_1$$ خواهیم رسید.
$$B_1=\dfrac{\frac{Q_3+Q_1}{2}-Q_2}{\frac{Q_3-Q_1}{2}}$$
چولگی G1
در محاسبه چولگی در بیشتر نرمافزارهای آماری نظیر SPSS، Minitab یا Excel از شیوه محاسبه زیر که توسط گیل (C. A. Gill) در سال 1998 ابداع شده، استفاده میشود.
$$G_1=\dfrac{\sqrt{n(n-1)}}{n-2}\times\dfrac{\tfrac{1}{n}\sum(x_i-\overline{x})^3}{(\dfrac{1}{n-1}\sum(x_i-\overline{x})^2)^\tfrac{3}{2}}$$
به سادگی دیده میشود که بین G1 و b1 رابطه زیر برقرار است.
$$G_1=\dfrac{n^2}{(n-1)(n-2)}b_1$$
ولی اگر تعداد مشاهدات زیاد باشد (n بزرگ باشد) مقدار G1 و b1 باهم برابر خواهند بود.
مثال
با توجه به دادههای نمونهای $$x={8,5,3,6,8,8,10,19,16,30}$$ ضرایب چولگی پیرسون و چارکی طبق جدول زیر ارائه شده است. البته تصویر مربوط به منحنی توزیع احتمال این دادهها نیز در شکل دیده میشود.
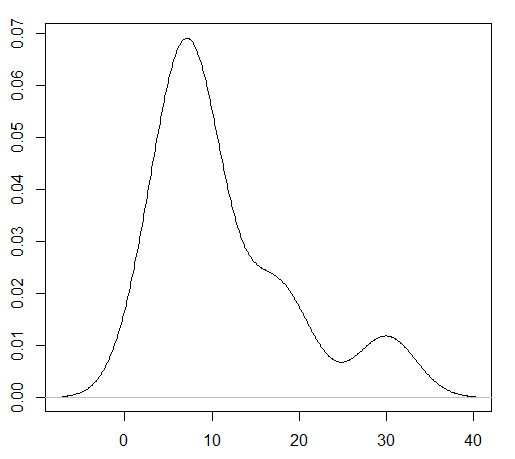
| روش محاسبه چولگی | چولگی گشتاوری | ضریب اول چولگی پیرسون | ضریب دوم چولگی پیرسون | چولگی برمبنای چارک |
| مقدار چولگی | b1 = 0.4152 G1 =0.5767 | 0.4035 | 0.4253 | 0.6250 |
این مطلب با ذکر منبع از سایت فرادرس بارگزاری شده است. لذا تمام حقوق مادی و معنوی این نوشته متعلق به تیم فرادرس میباشد.




