مقدار احتمال (p-Value) — معیاری ساده برای انجام آزمون فرض آماری

در بیشتر نرم‌افزارهای آماری برای سهولت در تصمیم‌گیری نسبت به نتیجه آزمون فرض آماری، شاخصی به نام «مقدار احتمال» (p-Value) ارائه می‌شود. این مقدار به محقق کمک می‌کند که بدون مراجعه به جداول توزیع‌های آماری بتواند در مورد رد یا عدم رد فرض صفر تصمیم بگیرید. گاهی به p-Value «احتمال با معنایی» (Significant Level) یا p-مقدار نیز می‌گویند. برای مثال در نرم‌افزار R‌ مقدار احتمال با p-Value و در نرم‌افزار SPSS مقدار احتمال با Sig نشان داده می‌شود.

مقدار احتمال (p-Value)

برای آنکه بتوان درک مناسبی از مقدار احتمال بدست آورد، ابتدا باید در مورد آزمون فرض آماری و مراحل انجام آن اطلاع داشت.

محاسبه مقدار احتمال برمبنای فرض صفر انجام می‌گیرد و از فرض مقابل استفاده‌ای نمی‌شود. بنابراین برمبنای مقدار احتمال می‌توان به رد فرض صفر ($H_0$) اقدام کرد. ولی باید توجه داشت که مقدار احتمال نمی‌تواند برای قبول فرض مقابل ($H_1$) معیار مناسبی باشد.

برای مثال یک آزمون فرض آماری را با فرضیات زیر برای پارامتر میانگین جامعه آماری، در نظر بگیرید:

$\begin{cases} H_0: \mu =10\\ H_1: \mu= 20\\ \end{cases}$

اگر فرض کنیم که براساس مقدار احتمال، فرض صفر رد شده است، مشخص نیست فرضیه‌ای که قبول خواهد شد حتما $H_1$ باشد. زیرا فرض مقابل می‌تواند هر یک از حالت‌های زیر باشد:

$\begin{cases} H_0: \mu =10\\ H_1: \mu< 20\\ \end{cases}$

$\begin{cases} H_0: \mu =10\\ H_1: \mu> 20\\ \end{cases}$

$\begin{cases} H_0: \mu =10\\ H_1: \mu= 30\\ \end{cases}$

بنابراین رد فرض صفر به معنی قبول فرض مقابل نخواهد بود.

حال برای تعریف غیررسمی از مقدار احتمال، فرضیات زیر را در نظر می‌گیریم:

• X آماره آزمون است.
• x حاصل آماره آزمون برحسب نمونه تصادفی است.
• ناحیه بحرانی نیز به صورت X>x نوشته شده.

تعریف غیر رسمی مقدار احتمال: احتمال رد فرض صفر (براساس نمونه تصادفی و آماره آزمون و ناحیه بحرانی) به شرط آنکه فرض صفر صحیح باشد، مقدار احتمال نامیده می‌شود. بیان ریاضی برای این حالت به صورت زیر است:

p-Value=$P(X >x|\;H_0)$

برای درک بهتر به یک مثال می‌پردازیم.

مثال ۱

در یک بازی شانسی، باید یک سکه پرتاب شود. اگر سکه شیر بیاید برنده خواهیم بود و در غیر اینصورت بازنده. برگزار کننده این بازی ادعا دارد که سکه‌اش نااریب است. یعنی احتمال ظاهر شدن شیر با خط برابر است. برای اینکه ادعای برگزار کننده را بررسی کنیم یک آزمون آماری تشکیل می‌دهیم.

اگر p احتمال مشاهده شیر باشد، فرضیه‌های این آزمون آماری به صورت زیر است:

$\begin{cases} H_0: p =\dfrac{1}{2}\\ H_1: p > \dfrac{1}{2}\\ \end{cases}$

حال اگر X را تعداد شیر در ۱۰ بار پرتاب سکه در نظر بگیریم، با انجام این آزمایش، نتیجه آماره آزمون (یعنی همان X) براساس نمونه تصادفی (شمارش تعداد شیرها در ۱۰ بار پرتاب سکه) برابر با 6 شده است.

حال مقدار احتمال را محاسبه می‌کنیم.

$P(X > 6|\;H_0)=۱-P(X\leq 5|\;p=\tfrac{1}{2})=$

$1-(\sum_{i=1}^5 {10 \choose i}\tfrac{1}{2}^i\times \tfrac{1}{2}^{10-i})=1-0.6230=0.3770$

این احتمال نشان می‌دهد که آزمون با صحیح بودن فرض صفر، چقدر وجود چنین نمونه‌ای را محتمل می‌داند. از آنجایی که این احتمال بزرگ به نظر می‌رسد، نمی‌توان فرض صفر را رد کرد.

همانطور که دیده شد وجود یا عدم وجود فرض مقابل تاثیری در محاسبه مقدار احتمال نداشت و با وجود فرض صفر، فقط ناحیه بحرانی و مقدار آماره آزمون برحسب نمونه تصادفی برای محاسبه مقدار احتمال کافی بود.

تعریف رسمی مقدار احتمال: کمترین مقداری از احتمال خطای نوع اول (سطح آزمون) که ممکن است یافته آماره آزمون، موجب رد فرض صفر شود.

به بیان دیگر، در یک آزمون فرض، مقدار احتمال (p-Value) برابر با کمترین مقداری از سطح معنی‌داری (significance level) یا همان احتمال خطای نوع اول است، که موجب رد فرض صفر می‌شود.

با توجه به این موضوع، می‌توان قاعده‌ای برای انجام آزمون فرض آماری بوسیله مقدار احتمال در نظر گرفت: فرض صفر رد می‌شود، هر گاه مقدار احتمال از $\alpha$ (احتمال خطای نوع اول) کوچکتر باشد.

شیوه محاسبه مقدار احتمال

در حالت کلی می‌توان مقدار احتمال را براساس نوع آزمون فرض برای پارمتر $\theta$ به صورت زیر محاسبه کرد.

در حالتی که آزمون فرض به صورت:

$\begin{cases} H_0: \theta =\theta_0\\ H_1: \theta > \theta_0\\ \end{cases}$

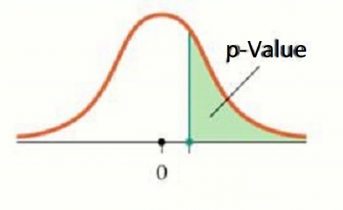
مقدار احتمال به صورت زیر محاسبه می‌شود:

p-Value=$P_{\theta_0}(X\geq x)$

همچنین در حالتی که آزمون فرض به شکل:

$\begin{cases} H_0: \theta =\theta_0\\ H_1: \theta < \theta_0\\ \end{cases}$

مقدار احتمال به صورت زیر خواهد بود:

p-Value=$P_{\theta_0}(X\leq x)$

همینطور در حالتی که آزمون فرض به صورت:

$\begin{cases} H_0: \theta =\theta_0\\ H_1: \theta \neq \theta_0\\ \end{cases}$

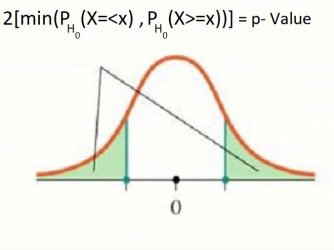
مقدار احتمال به صورت زیر قابل محاسبه است:

p-Value=$2\min(P_{\theta_0}(X\leq x),P_{\theta_0}(X\geq x))$

مثال ۲

متغیر تصادفی تعداد زدگی‌ها در یک توپ پارچه، دارای توزیع پواسن با پارامتر $\lambda$ است. طبق نظر کارشناس کارخانه متوسط تعداد زدگی در هر توپ پارچه برابر با ۵ است. به طور تصادفی یک توپ از پارچه‌ها انتخاب شده و تعداد زدگی‌ها برابر با ۱۰ شمارش شده است. در سطح خطای ۵٪، گفته کارشناس را بررسی می‌کنیم.

می‌دانیم تعداد زدگی‌ها (X) دارای توزیع پواسن با پرامتر $\lambda$‌ است. یعنی $X\sim P(\lambda)$.

حال با توجه به اینکه نظر کارشناس، گزاره‌ای است که از قبل در مورد پارامتر جامعه وجود داشته، فرض‌های مربوط به آزمون آماری را می‌نویسیم.

$\begin{cases} H_0: \lambda =5\\ H_1: \lambda \neq 5\\ \end{cases}$

بنابراین مقدار احتمال به صورت زیر قابل محاسبه است:

$P_{\lambda=5}(X\leq 10)=\sum_{k=1}^{10} \dfrac{e^{-5}5^k}{k!}=0.9863$

و همچنین:

$P_{\lambda=5}(X\geq 10)=1-P_{\lambda=5}(X\leq 9)=1-(\sum_{k=1}^{9} \dfrac{e^{-5}5^k}{k!})=1-0.9682=0.0318$

در نتیجه خواهیم داشت:

p-Value=$2\min(P(X\leq 10),P(X\geq 10))=2\min(0.9863,0.0318)=0.0636$

از آنجایی که در سطح خطای 0.05 (۵٪) آزمون باید انجام شود، با مقایسه مقدار احتمال و سطح خطا متوجه می‌شویم که فرض صفر رد نمی‌شود. زیرا 0.0636 > 0.05 است.

مشکلات در تفسیر مقدار احتمال

اغلب در بیان توصیفی که مقدار احتمال ارائه می‌کند، مشکلاتی در بین دانشجویان دیده می‌شود.

• مقدار احتمال، احتمال خطای نوع اول نیست. زیرا این مقدار براساس نمونه تصادفی محاسبه می‌شود ولی احتمال خطای نوع اول براساس متغیر تصادفی آماره آزمون بدست می‌آید.
• از مقدار احتمال به عنوان یک معیار استفاده می‌شود و نمی‌توان از آن تفسیرهایی که در ادامه آمده است را ارائه داد؛ مثلا اگر مقدار احتمال نزدیک $\alpha$ بود نباید گفته شود که «تقریبا در بیشتر مواقع فرض صفر رد می‌شود» یا فاصله زیاد مقدار احتمال با $\alpha$ باعث شود که بگوییم «با اطمینان زیاد می‌توان فرض صفر را رد کرد» و … .

^^