آزمون فرض میانگین جامعه در آمار
در آمار استنباطی یکی از مهمترین و معمولترین روشها، استفاده از آزمون آماری است. با استفاده از این روش، قادر هستیم در مورد پارامتر جامعه آماری براساس یک آزمون، قضاوت کنیم. این کار به کمک تحلیل روی نمونه تصادفی صورت گرفته و به محقق در تصمیمگیری در مورد پارامتر جامعه آماری یاری میرساند.
آزمون فرض میانگین جامعه نرمال
هدف اصلی در آزمون فرض برای میانگین جامعه، تصمیم در مورد مقدار یا حدود میانگین جامعه است. بنابراین میتوان از آزمونهای ساده یا مرکب، یک طرفه یا دو طرفه برای این کار استفاده کرد.
فرض کنید آزمون مورد نظر از دو فرض صفر و فرض مقابل که به صورت زیر نوشته شدهاند تشکیل شده است.
$\begin{cases} H_0: \mu =\mu_0 \\ H_1: \mu= \mu_1\\ \end{cases}$
باید توجه داشت که هر دو مقدار $\mu_0$ و $\mu_1$ معلوم هستند و داریم $\mu_0<\mu_1$. از آنجایی که هم فرض صفر و هم فرض مقابل توزیع جامعه را مشخص میکنند، به آنها فرضیههای ساده گفته شده و این آزمون فرض به صورت فرض ساده در مقابل ساده خوانده میشود.
برای انجام این آزمون احتیاج به یک آماره آزمون داریم. همانطور که میدانید، آماره آزمون باید به پارامتر مجهول جامعه ($\mu$) وابسته نباشد. به این منظور دو حالت را در نظر میگیریم:
- زمانی که واریانس جامعه معلوم و مشخص باشد
- زمانی که واریانس مشخص نیست و باید از برآورد آن در آماره آزمون استفاده کرد.
آزمون فرض میانگین جامعه نرمال با معلوم بودن واریانس جامعه
در این حالت با معلوم بودن واریانس جامعه آماری، آماره آزمون Z را به صورت زیر تحت فرض $H_0$ در نظر میگیریم:
$Z=\dfrac{\overline{X}-\mu_0}{\frac{\sigma}{\sqrt{n}}}$
همانطور که دیده میشود، متغیر تصادفی Z تحت فرض $H_0$ به پارامتر مجهول وابسته نیست و توزیع آن نیز نرمال با میانگین صفر و واریانس 1 است. در نتیجه Z را آماره آزمون نامیده و ناحیه بحرانی را براساس آن ایجاد میکنیم. با توجه به فرض و شرطی که بین مقدار $\mu_0$ و $\mu_1$ وجود دارد ناحیه بحرانی را به صورت زیر تعریف میکنیم:
$Z=\dfrac{\overline{X}-\mu_0}{\frac{\sigma}{\sqrt{n}}}>c$
این ناحیه بحرانی نشان میدهد که اگر اختلاف میانگین نمونه از مقدار $\mu_0$ زیاد باشد (به ازاء هر واحد از انحراف استاندارد) به رد فرض صفر رای میدهیم. مقدار c را نیز با توجه به تعریف احتمال خطای نوع اول ($\alpha$) به صورت زیر بدست میآوریم.
$\alpha=P(Reject\; H_0\;| H_0\; is \ true)=P(Z>c)=1-\Phi(c)$
در این رابطه $\Phi(c)$ مقدار تابع توزیع احتمال نرمال استاندارد در نقطه c است. در نتیجه مقدار c را با استفاده از رابطه زیر بدست میآوریم:
$\Phi(c)=1-\alpha\rightarrow\; c=z_{1-\alpha}$
به این ترتیب میتوان ناحیه بحرانی را به صورت $Z>z_{(1-\alpha)}$ نوشت. پس فرض $H_0$ را رد میکنیم اگر مقدار آماره آزمون Z بزرگتر از صدک ($1-\alpha$) توزیع نرمال استاندارد باشد.
البته باید توجه داشت که با تغییر فرض مقابل ممکن است ناحیه بحرانی به شکل دیگری نوشته شود. در زیر به چند حالت از فرض مقابل و ناحیه بحرانی مربوطه اشاره میکنیم:
| ناحیه بحرانی | آماره آزمون | فرض مقابل | فرض صفر |
| $Z>z_{(1-\alpha)}$ | $Z=\dfrac{\overline{X}-\mu_0}{\frac{\sigma}{\sqrt{n}}}$ | $\mu=\mu_1 ,\;\;\;\;\mu_1>\mu_0$ | $\mu=\mu_0$ |
| $Z<-z_{(1-\alpha)}$ | $Z=\dfrac{\overline{X}-\mu_0}{\frac{\sigma}{\sqrt{n}}}$ | $\mu<\mu_0 $ | $\mu=\mu_0$ |
| $|Z|>z_{(1-\frac{\alpha}{2})}$ | $Z=\dfrac{\overline{X}-\mu_0}{\frac{\sigma}{\sqrt{n}}}$ | $\mu\neq\mu_0$ | $\mu=\mu_0$ |
در سطرهای اول و دوم، نوع آزمون یک طرفه و در سطر سوم آزمون دو طرفه در نظر گرفته شده است. همچنین در این جدول فرض صفر به صورت فرض ساده نوشته شده است.
نکته: اگر بتوان توزیع جامعه را نرمال فرض کرد و واریانس جامعه نیز معلوم باشد از آزمون Z استفاده میشود. در عمل زمانی که تعداد مشاهدات بیشتر از ۳۰ باشند میتوان توزیع Z را نرمال فرض کرد. در غیر اینصورت بهتر است از آزمونهای مربوط به آماره T استفاده شود.
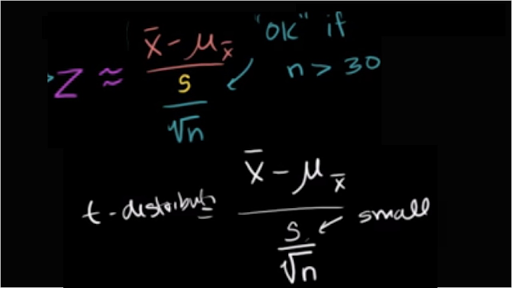
مثال ۱
جامعه آماری، از پسرانی که در محدوده سنی 10 تا 12 سال هستند تشکیل شده است. اطلاعات قبلی نشان میدهد که متوسط قد این افراد برابر است با 75 سانتیمتر و واریانس جامعه آماری برای قد این پسران برابر است با $11.6^2$ سانتیمتر مربع. با توجه به تغییر شیوه تغذیه اعتقاد داریم که میانگین قد پسرها در جامعه افزایش داشته و به 80 سانتیمتر رسیده است. براساس یک نمونه ۲۵ تایی میانگین قدها برابر با 80.94 سانتیمتر بدست آمده است. آیا میتوان از اطلاعات قبلی در مورد قد اطمینان داشت یا میتوان به کمک آزمون آماری نشان داد که تغییر محسوسی در میزان قد پسران رخ داده است؟
برای پاسخ به این سوال دست به یک آزمون آماری میزنیم. فرضیات این آزمون به صورت زیر نوشته میشود:
$\begin{cases} H_0: \mu =75\\ H_1: \mu= 80\\ \end{cases}$
همانطور که گفته شد، فرضیه صفر، نتایج و نظراتی که از قبل وجود داشته را بیان کرده ولی فرض مقابل نظر محقق را نشان میدهد. سعی داریم به کمک نمونه تصادفی تهیه شده، در مورد فرض صفر قضاوت کنیم. با توجه به آماره آزمون معرفی شده و ناحیه بحرانی آزمون فرض را انجام میدهیم.
$Z=\dfrac{\overline{X}-\mu_0}{\frac{\sigma}{\sqrt{n}}}=$
$Z=\dfrac{80.94-75}{\frac{11.6}{\sqrt{25}}}=$
$Z=\dfrac{5.94}{2.32}=2.56$
اگر میزان احتمال خطای نوع اول را $\alpha=0.05$ در نظر بگیریم، خواهیم داشت:
$Z>z_{(1-\alpha)}=2.56>1.64$
در نتیجه با خطای 0.05، رای به رد فرض $H_0$ میدهیم.

آزمون فرض میانگین جامعه نرمال با نامعلوم بودن واریانس جامعه
در این حالت با توجه به اینکه واریانس جامعه نامعلوم است، باید از برآورد آن در آماره آزمون استفاده کرد. به همین دلیل آماره آزمون دیگر دارای توزیع نرمال نخواهد بود. اگر برآورد واریانس جامعه را با $S^2$ نشان دهیم، خواهیم داشت:
$S^2=\dfrac{\sum_{i=1}^n (X_i-\overline{X})}{n-1}$
$S^2$، برآوردگر نااریب برای واریانس جامعه است. براساس این برآوردگر آماره آزمونT را به صورت زیر در نظر میگیریم:
$T=\dfrac{\overline{X}-\mu_0}{\frac{S}{\sqrt{n}}}$
حال فرض کنید آزمون مورد نظر از دو فرض صفر و فرض مقابل که به صورت زیر نوشته شدهاند تشکیل شده است.
$\begin{cases} H_0: \mu =\mu_0 \\ H_1: \mu= \mu_1\\ \end{cases}$
همانطور که دیده میشود، آماره آزمون مورد نظر (T) یک متغیر تصادفی است که تحت فرض $H_0$ به پارامتر مجهول وابسته نیست و دارای توزیع t-student با n-1 درجه آزادی است. این آماره توسط «ویلیام گوست» (William Gosset) شیمیدان و آماردان انگلیسی در سال 1908 معرفی و در آزمونهای آماری بسیاری به کار گرفته شد.

با توجه به فرضیات مربوط به آزمون فرض که به صورت ساده در مقابل ساده نوشته شده است میتوان ناحیه بحرانی را به صورتی در نظر گرفت که با بزرگ شدن آماره آزمون فرض صفر رد شود. در نتیجه ناحیه بحرانی با توجه به احتمال خطای نوع اول ($\alpha$) در این حالت به صورت زیر در خواهد آمد.
$\alpha=P(Reject\; H_0\;| H_0\; is \ true)=P(T>c)=1-P(T\leq c)$
$1-\alpha=P(T\leq c)$
بنابراین ناحیه بحرانی برابر است با $T>t_{1-\alpha}(n-1)$. پس اگر مقدار T براساس نمونه از مقدار صدک $1-\alpha$ توزیع t با n-1 درجه آزادی بزرگتر باشد، به رد فرض صفر رای میدهیم.
البته باید توجه داشت که با تغییر فرض مقابل ممکن است ناحیه بحرانی به شکل دیگری نوشته شود. در زیر به چند حالت از فرض مقابل و ناحیه بحرانی مربوطه اشاره میکنیم:
| ناحیه بحرانی | آماره آزمون | فرض مقابل | فرض صفر |
| $T>t_{(1-\alpha)}(n-1)$ | $T=\dfrac{\overline{X}-\mu_0}{\frac{s}{\sqrt{n}}}$ | $\mu=\mu_1 ,\;\;\;\;\mu_1>\mu_0$ | $\mu=\mu_0$ |
| $T<-t_{(1-\alpha)}(n-1)$ | $T=\dfrac{\overline{X}-\mu_0}{\frac{s}{\sqrt{n}}}$ | $\mu<\mu_0 $ | $\mu=\mu_0$ |
| $|T|>t_{(1-\frac{\alpha}{2})}(n-1)$ | $T=\dfrac{\overline{X}-\mu_0}{\frac{s}{\sqrt{n}}}$ | $\mu\neq\mu_0$ | $\mu=\mu_0$ |
در سطرهای اول و دوم نوع آزمون یک طرفه و در سطر سوم آزمون دو طرفه در نظر گرفته شده است. همچنین در این جدول فرض صفر به صورت فرض ساده نوشته شده است.
مثال ۲
یک شرکت تولید کننده موتورسیکلت ادعا دارد که میزان مصرف سوخت تولیداتش در هر ۱۰۰ کیلومتر برابر با 2 لیتر است. به این منظور سازمان بهینهسازی مصرف سوخت، ۸ موتورسیکلت از این شرکت را به منظور بررسی ادعایش تحویل گرفته. اطلاعات مربوط به مصرف سوخت این ۸ دستگاه در جدول زیر آورده شده است. در سطح خطای $\alpha=0.05$ ادعای تولید کننده بررسی میشود.
| شماره نمونه | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| مصرف سوخت | 3.0 | 2.8 | 3.2 | 2.6 | 3.3 | 2.5 | 2.8 | 3.0 |
با توجه به اطلاعات جدول، میانگین و انحراف معیار نمونه محاسبه شده و آماره آزمون بدست میآید.
$\overline{X}=2.9,\;\;\;s(X)=0.278,\;\;\;n=8$
حال آماره آزمون را محاسبه کرده و در ناحیه بحرانی قرار میدهیم.
$T=\dfrac{\overline{X}-\mu_0}{\frac{s}{\sqrt{n}}}=$
$\dfrac{2.9-2}{\frac{0.278}{\sqrt{8}}}=9.165$
با توجه به صدک 95ام از توزیع T با $8-1=7$ درجه آزادی که برابر با 1.895 است، میبینیم که آماره آزمون در ناحیه بحرانی قرار گرفته و فرض صفر رد میشود زیرا $9.165<1.895$ پس ادعای کارخانه تولید کننده موتورسیکلت رد میشود.




